Genius 算法引擎

适用场景：

卷积神经网络(Convolutional Neural Networks， ConvNets or CNNs)是一种在图像识别与分类领域被证明特别有效的神经网络。典型应用场景包括语音识别、人脸识别、通用物体识别、运动分析、自然语言处理甚至脑电波分析方面均有突破。

算法思想：

Hubel和Wiesel在对猫视觉皮层用于局部敏感和方向选择的神经元时发现其独特的网络结构，它可以有效地降低反馈神经网络的复杂性。受到这一发现的启发有人提出了卷积神经网络（CNN）。

卷积神经网络与普通神经网络的区别在于卷积神经网络包含了一个由卷积层和子采样层构成的特征抽取器。在卷积神经网络的卷积层中，一个神经元只与部分邻层神经元连接。在CNN的一个卷积层中，通常包含若干个特征平面(featureMap)，每个特征平面由一些矩形排列的的神经元组成，同一特征平面的神经元共享权值，这里共享的权值就是卷积核。

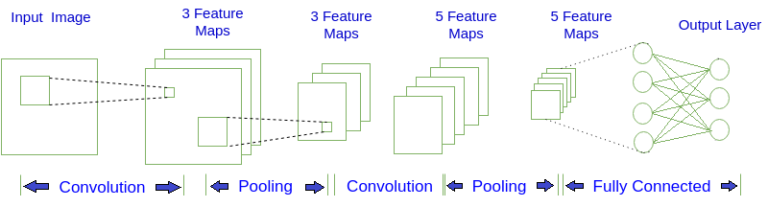
● 卷积核一般以随机小数矩阵的形式初始化，在网络的训练过程中卷积核将学习得到合理的权值。
● 子采样也叫做池化（pooling），通常有均值子采样（mean pooling）和最大值子采样（max pooling）两种形式。子采样可以看作一种特殊的卷积过程。卷积和子采样大大简化了模型复杂度，减少了模型的参数。

卷积神经网络的基本结构如图所示：

CNN 工作原理本质上分为两个阶段：卷积操作和池化操作。

卷积操作：一种混合信息的手段。比如与两个装满信息的桶：第一个桶内是输入的图像，由三个矩阵构成，即 RGB 三通道，其中每个元素都是 0 到 255 之间的一个整数。第二个桶内是卷积核，其实就是单个浮点数矩阵。这里我们将卷积核的大小和模式，想象成一个搅拌图像的方法，用它到第一个桶中搅拌混合，输出一幅修改后的图像，在深度学习中，这就经常被我们称作特征图（Feature Map）。对于每个颜色通道，都有一个特征图。所以具体来说，卷积操作就是从输入图片中取出一个与卷积核大小相同的区块，比如图片为 6×6，卷积核大小为 3×3，那么我们取出的区块大小就是 3×3。然后对每对相同位置的元素，执行乘法后求和（不同于矩阵乘法，却类似向量内积，这里是两个相同大小的矩阵的“点乘”），由此乘积的和就生成了特征图中的一个像素。当一个像素计算完毕后，移动一个像素取下一个区块执行相同的运算。当无法再移动取得新区块时，对特征图的计算就结束了。由此可见，卷积就是一种数学运算，类似向量内积，是两个相同大小的矩阵的“点乘”，这种运算有助于简化更复杂的表达式。

池化操作：池化层（Pooling Layer）一般在卷积层后面（卷积层对应上面的隐藏层），该层的目的是为了简化卷积层的训练输出数据。如上所述，整个图像的这种“卷积”会产生大量的信息。而进入池化层，可将其全部缩小成更通用和可处理的形式。现有池化技术有很多，其中最受欢迎的是“最大池”（Maxpooling），池化层的每一个神经元的值对应卷积层的 2×2 的区域的最大输出值。它将每个特征图编辑成自己的数据字典，因此只有红色、茎、或者曲线的最好样本被表征出来。

CNN 算法成功的关键在于：采用局部连接方法和分享权值方法，降低了参数数目，在图像处理上体现出优越性，也更接近于实际的生物神经网络。除了降低参数数目以外，CNN 还采用了特征提取，从而避免了对图像的复杂前期预处理，可以直接输入原始图像。

CNN算法流程描述为：
输入层->卷积层->激励函数(relu)->池化层->全连接层->输出层

● 第一层输入图片, 进行卷积(Convolution)操作, 得到第二层深度为 3 的特征图(Feature Map)
● 对第二层的特征图进行池化(Pooling)操作, 得到第三层深度为 3 的特征图
● 重复上述操作得到第五层深度为 5 的特征图, 最后将这 5 个特征图, 也就是 5 个矩阵, 按行展开连接成向量, 传入全连接(Fully Connected)层, 全连接层就是一个 BP 神经网络
● 图中的每个特征图都可以看成是排列成矩阵形式的神经元, 与 BP神经网络中的神经元大同小异

案例1：

(卷积)对于一张输入图片，将其转化为矩阵，矩阵的元素为对应的像素值。假设有一个 5×55×5 的图像，使用一个 3×33×3 的卷积核进行卷积，可得到一个 3×33×3 的特征图。卷积核也称为滤波器(Filter)。

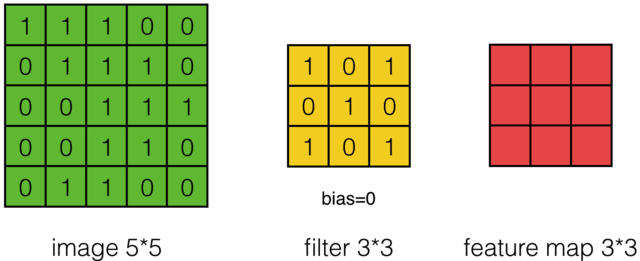
具体的操作过程如下图所示：

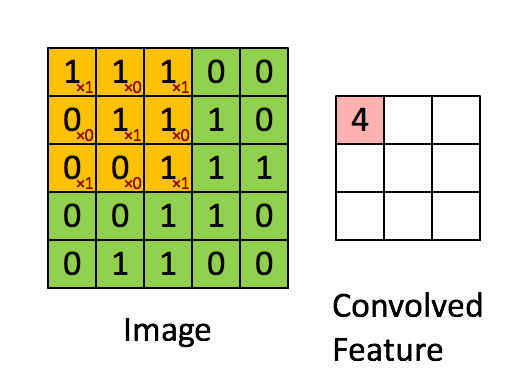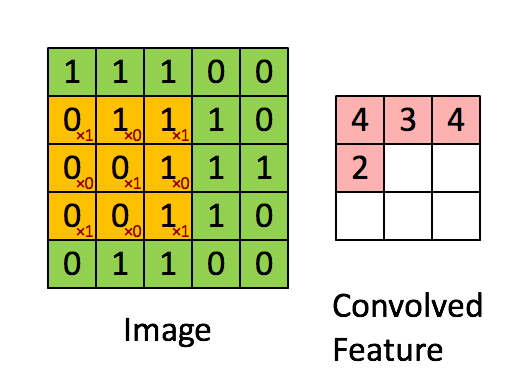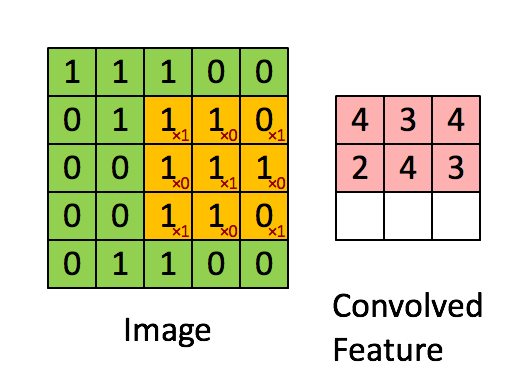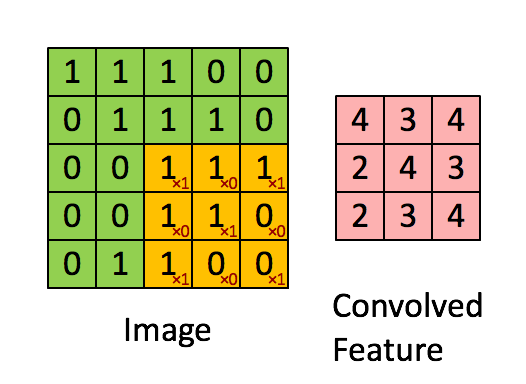
黄色的区域表示卷积核在输入矩阵中滑动，每滑动到一个位置，将对应数字相乘并求和，得到一个特征图矩阵的元素。注意到，动图中卷积核每次滑动了一个单位，实际上滑动的幅度可以根据需要进行调整。

为了提取更多的特征，可以采用多个卷积核分别进行卷积，这样便可以得到多个特征图。有时，对于一张三通道彩色图片，或者如第三层特征图所示，输入的是一组矩阵，这时卷积核也不再是一层的，而要变成相应的深度。

(池化)池化又叫下采样(Down sampling), 与之相对的是上采样(Up sampling). 卷积得到的特征图一般需要一个池化层以降低数据量. 池化的操作如下图所示:

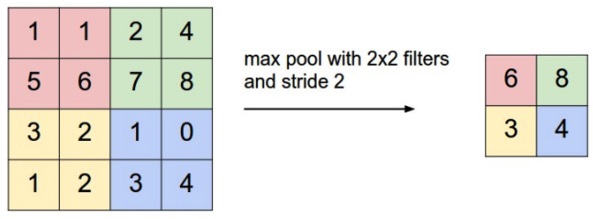
和卷积一样, 池化也有一个滑动的核, 可以称之为滑动窗口, 上图中滑动窗口的大小为 2×2, 步幅为 2, 每滑动到一个区域, 则取最大值作为输出, 这样的操作称为 Max Pooling. 还可以采用输出均值的方式, 称为 Mean Pooling。

(全连接)经过若干层的卷积, 池化操作后, 将得到的特征图依次按行展开, 连接成向量, 输入全连接网络。

案例2：

下面演示的是用MNIST数字数据集训练卷积神经网络，数据集非常简单，可以在几分钟内达到99％左右的准确度。

该网络输入28x28的MNIST数据集图像，在训练之前会利用5x5的滤波器对图像进行处理得到24x24的图像。在有chrome浏览器的机器上，网络的向前传播与训练都大约需要5ms。默认情况下，使用的是Adadelta自适应学习率调整，因此不必担心随着时间的推移需要改变学习率。

补充说明

一个 CNN 是为了识别二维形状而特殊设计的多层感知器, 对二维形状的缩放, 倾斜或其它形式的变形具有高度不变性. 每一个神经元从上一层的局部区域得到输入, 这迫使神经元提取局部特征. 一旦一个特征被提取出来, 它相对于其它特征的位置被近似保留下来, 而忽略掉精确的位置. 每个卷积层后面跟着一个池化, 使得特征图的分辨率降低, 而有利于降低对二维图形的平移或其他形式的敏感度。

权值共享是 CNN 的一大特点, 每一个卷积核滑遍整个输入矩阵, 而参数的数目等于卷积核矩阵元素的数目加上一个偏置, 相对于 BP 网络大大减少了训练的参数. 例如对于一张300×300 的彩色图片, 如果第一层网络有25个神经元, 使用 BP网络, 参数的数目可达 675万个(300×300×3×25+1), 而卷积网络只有76个(25×3+1)。

每一个卷积核就是一个特征提取器, 可以提取出输入图片或特征图中形状, 颜色等特征. 当卷积核滑动到具有这种特征的位置时, 便会产生较大的输出值, 从而达到激活的状态。

算法优点

● 共享卷积核，对高维数据处理无压力
● 需手动选取特征，训练好权重，即得特征分类效果好

算法缺点

● 需要调参，需要大样本量，训练最好要GPU
● 物理含义不明确